Ray Tracing 004The Ray Class

Summary

Math foundations: ray as a line in 3D space from an origin pointing into a direction.
Added a ray class to help compute coordinates of a point on the ray at a given time.
Updated to let the ray draw a gradient from blue to white along the y-coordinate.

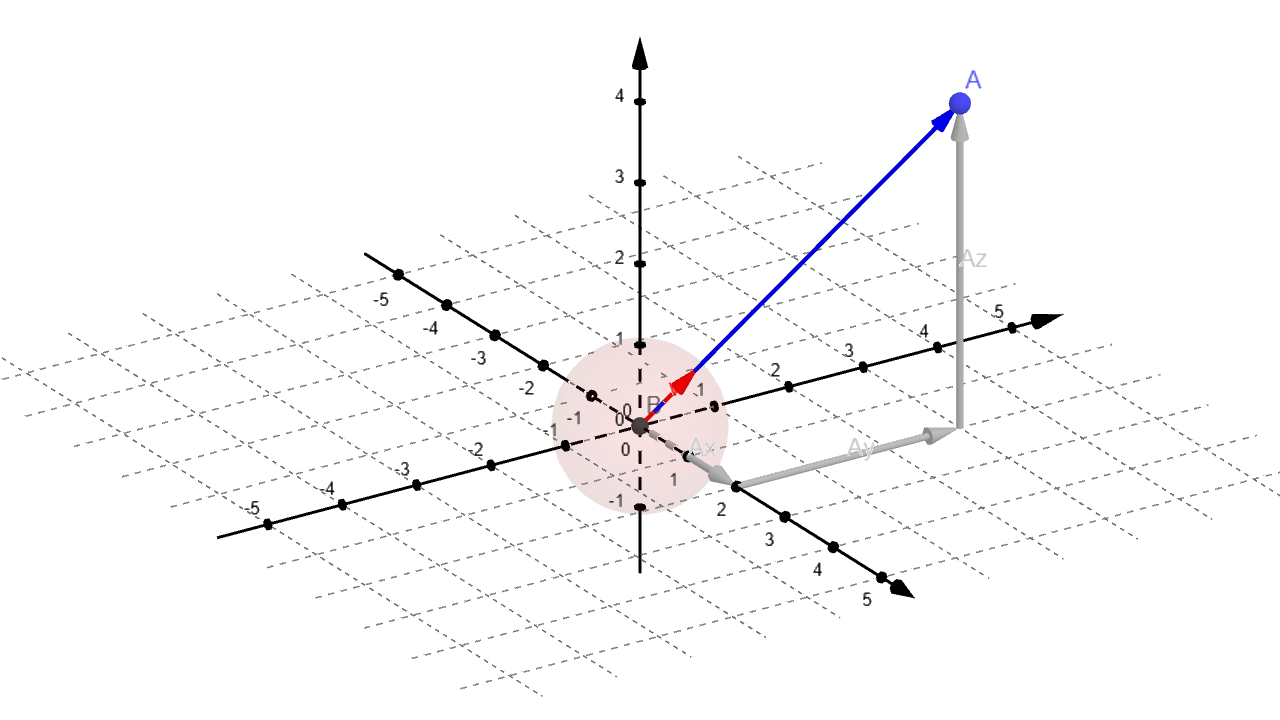
A ray can be thought of as a function:

\begin{equation} p(t) = A + t * B \end{equation}

where p is a 3D position along a line, A is the ray origin, B is the ray direction, and t is the ray parameter which moves p(t) along the ray.

If t is positive you get the points in front of the origin A, also called a half-line or half-ray.

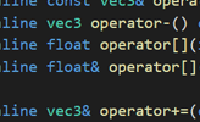
The ray class is a literal translation of this equation in 3D vectors:

// ray.h
#ifndef RAYH
#define RAYH
#include "vec3.h"

class ray {
public:
  vec3 A;
  vec3 B;

  ray() {}
  ray(const vec3& a, const vec3& b) { A = a; B = b; }

  vec3 origin() const { return A; }
  vec3 direction() const { return B; }
  vec3 point_at_parameter(float t) const { return A + t * B; }
};
#endif

The new loop in the main program moves the ray across the entire image and determines a color at each pixel. This example will only return a gradient based on the y-position.

The size of the image is set to 4 by 2, where the origin is set into the center of image (0,0,0), the lower left corner is at (-2,-1,-1), the upper right corner is at (2,1,-1). The z-coordinate is set at -1 into the screen to respect the convention of a right-handed coordinate system.

The screen is 1 unit apart from the origin (eye or camera). Positive values for z are behind the camera.

Click to view C++ source code

// ray-example.cpp
#include <iostream&gt;
#include "vec3.h"
#include "ray.h"

[HL]
vec3 color(const ray& r) {
  vec3 unit_direction = unit_vector(r.direction());
  float t = 0.5f * (unit_direction.y() + 1.0f);
  return (1.0f - t) * vec3(1.0f, 1.0f, 1.0f) + t * vec3(0.5f, 0.7f, 1.0f);
}
[/HL]

int main() {
  int nx = 200;
  int ny = 100;

  std::cout << "P3\n" << nx << " " << ny << "\n255\n";
  
  [HL]
  vec3 lower_left_corner(-2.0, -1.0, -1.0);
  vec3 horizontal(4.0, 0.0, 0.0);
  vec3 vertical(0.0, 2.0, 0.0);
  vec3 origin(0.0, 0.0, 0.0);
  [/HL]
  
  for (int j = ny-1; j &gt;= 0; j--) {
    for (int i = 0; i < nx; i++) {
      float u = float(i) / float(nx);
      float v = float(j) / float(ny);
      
      [HL]
      ray r(origin, lower_left_corner + u * horizontal + v * vertical);
      vec3 col = color(r);
      [/HL]

      int ir = int(255.99 * col[0]);
      int ig = int(255.99 * col[1]);
      int ib = int(255.99 * col[2]);

      std::cout << ir << " " << ig << " " << ib << "\n";
    }
  }
}

The color() function takes the current ray's direction and computes a unit-direction. This unit-direction is a vector of length 1.

The following math is more verbose than it needs to be, but because unit vectors play such an important role, I thought it would be a good idea to at least once describe in full detail how the unit vector is calculated. It can also serve as a refresher on notation and what exactly is behind the common vector symbols.

\begin{equation} \hat{\boldsymbol{u}} = \frac{\boldsymbol{u}}{|\boldsymbol{u}|} \end{equation}

\begin{equation} \boldsymbol{|u|} = \sqrt{u_x^2 + u_y^2 + u_z^2} \end{equation}

Example: For vector $\boldsymbol{u}$ :

\begin{equation} \boldsymbol{u} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} \end{equation}

the length of the vector $|\boldsymbol{u}|$ is approximately 5.39:

\begin{equation} \begin{aligned}|\boldsymbol{u}| & = \sqrt{2^2 + 3^2 + 4^2} \ & = \sqrt{4+9+16} \ & = \sqrt{29} \approx 5.39 \end{aligned} \end{equation}

The unit vector $\hat{\boldsymbol{u}}$ is:

\begin{equation} \hat{\boldsymbol{u}} = \frac{\boldsymbol{u}}{|\boldsymbol{u}|} = \begin{pmatrix} \frac{2}{\sqrt{29}} \\ \frac{3}{\sqrt{29}} \\ \frac{4}{\sqrt{29}} \end{pmatrix} \approx \begin{pmatrix} 0.37 \\ 0.56 \\ 0.74 \end{pmatrix} \end{equation}

To double-check correctness, the length of the unit vector should be 1:

\begin{equation} \begin{aligned}\left|\begin{pmatrix} 0.37 \\ 0.56 \\ 0.74 \end{pmatrix}\right| &= \sqrt{0.37^2 + 0.56^2 + 0.74^2} \\ &= \sqrt{0.14 + 0.31 + 0.55} \\ &= 1 \end{aligned} \end{equation}

Vector example, its components and the resulting unit vector

The y-component of this unit vector can take values from -1 to +1. To turn this into a range from 0 to 1, I add 1 to the value and divide it by 2.

The next line,

return (1.0f - t) * vec3(1.0f, 1.0f, 1.0f) + t * vec3(0.5f, 0.7f, 1.0f);

creates a linear interpolation (or "lerp") between white and blue. The first half of the equation turns 0 and leaves blue (0.5, 0.7, 1.0) when t is 1. The second half turns 0 and leaves white (1.0, 1.0, 1.0) when t is 0.

Each half will contribute to the final color for every t in between. Smaller t (y-coordinates towards the bottom of the image) result in brighter blue to white colors. Larger t (y-coordinates towards the top of the image) produce darker tones of blue.

Inside the loop I'm converting the pixel coordinates (from 0-199 in x-direction, from 0-99 in y-direction) to the world coordinate system (from -2 to +2 in x-direction, -1 to +1 in y-direction).

ray r(origin, lower_left_corner + u * horizontal + v * vertical);
vec3 col = color(r);

Javascript and Canvas

Here's the example in Javascript.

Figure RT004: Simple canvas image rendered with Javascript

Click to view Javascript source code

Gerrit Wessendorf 👋

Ray Tracing 004The Ray Class

Next Steps

Summary

Javascript and Canvas

Links

Next Steps